Distribuční funkce vzhledem k pravděpodobnostní míře
Předpokládejme, že \((M,d)\) je metrickým prostorem a nechť \({\cal T}\) označuje systém všech otevřených množin v \(M\). Nyní nejmenší sigma algebru obsahující systém všech otevřených množin \({\cal T}\) nazveme sigma algebrou Borelovských množin na \(M\).
Uvažujme pravděpodobnostní prostor \((S, {\cal A}, P)\), kde množina \(S\) nemusí být nutně konečnou množinou.
Definice.
Náhodnou veličinou na pravděpodobnostním prostoru \((S, {\cal A}, P)\) budeme rozumět reálnou funkci \(X:S\to\mathbb R\) takovou, že pro každou Borelovskou podmnožinu \(B\) reálných čísel platí:
\[
\{e\in S:X(e)\in B\}\in {\cal A}.
\]
Poznámka.
Abychom ověřili, že daná funkce \(X:S\to\mathbb R\) je skutečně náhodnou veličinou, stačí ukázat pro každé \(b\in\mathbb R\): \(\{e\in S:\ X(e)\le b\}\in{\cal A}\) nebo že
\[
\{e\in S:\ a\le X(e)\le b\}\ \ \textrm{ pro všchna } a,b\in\mathbb R.
\].
Příklad. Předpokládejme, že jsme náhodně vybrali náhodně osobu z jistého vzorku populace a změřili jsme výšku a hmotnost této osoby. Nyní uvažujme základní prostor \(S\) jako rovinu \({\mathbb R}^2\) uspořádaných dvojic reálných čísel \((x,y)\) s tím, že souřadnice \(x\) bude reprezentovat výšku osoby a druhá souřadnice \(y\) bude reprezentovat hmotnost osoby. Na \(S\) uvažujme sigma algebru Borelovských podmnožin, tj. \({\cal A} = {\cal B}\) = "sigma algebra Borelovských podmnožin euklidovského prostoru \({\mathbb R}^2\)." Dále předpokládejme, že \(X_1\) je výška náhodně vybrané osoby a \(X_2\) je hmotnost náhodně vybrané osoby. Nyní pro \(a,b\in\mathbb R\) je \[ \{(x,y):a\le X_1(x,y)\le b\} = \{(x,y):a\le x\le b\}. \] Tato množina je zřejmě Borelovskou množinou.
Klasifikace náhodných proměnných
Řekneme, že náhodná proměnná \(X\) je diskrétní náhodnou veličinou, jestliže obor hodnot je buď konečnou nebo spočetnou nekonečnou množinou. Jsou-li pak \(x_1, x_2\ldots\) jsou funkční hodnoty náhodné veličiny \(X\) které náleží do Borelovské množiny \(B\), potom je \[ P(\{e\in S:\ X(e)\in B\}) = \sum_i P(\{X = x_i\}) = \sum_{x\in B}p_X(x), \] kde \(p_X(x)\) je tzv. pravděpodobnostní funkce náhodné veličiny \(X\).
Připomeňme si co je to distrubuční funkce náhodné proměnné \(X\). Jedná se o funkci \(F_X: S\to\mathbb R\) definovaná předpisem:
\[
F_X(x) = P(\{X\le x\}), \ \ \ x\in\mathbb R.
\]
Podívejme se na obrázek různých druhů distribučních funkcí:
Obrázky distr. funkcí.
V diskrétním případě, známe-li pravděpodobnostní funkci \(p_X\), umíme pak sestrojit distribuční funkci \(F_X\) a naopak, známe-li distribuční funkci umíme pak sestrojit pravděpodobnostní funkci \(p_X\)
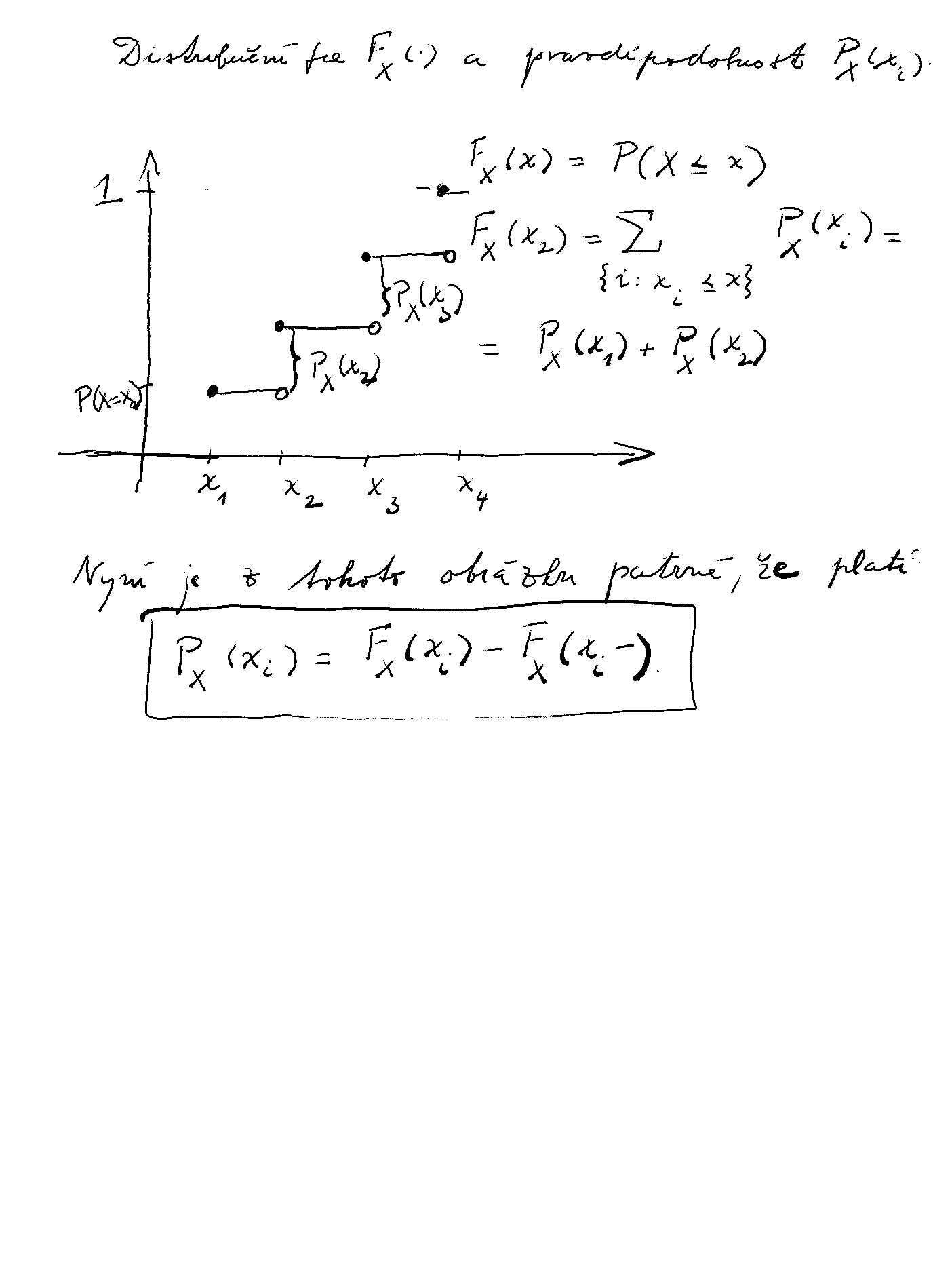 obrázek diskrétní distr. funkce
obrázek diskrétní distr. funkce
Definice. Řekneme, že náhodná veličina \(X\) je absolutně spojitá, existuje-li nezáporná funkce \(f_X:\mathbb R\to\mathbb R,\) taková, že platí: \[ F_X(x) = \int_{-\infty}^x f_X(t) dt, \ \ \ \textrm{ pro všechna } x. \] Funkci \(f_X\) budeme nazývat hustotou pravděpodobnosti náhodné veličiny \(X\).
Definice. Uvažujme pravděpodobnostní prostor \((\mathbb{R}, {\cal B}, P)\), kde \({\cal B}\) je sigma algebra všech Borelovských podmnožin množiny reálných čísel. Položíme-li \[ F(x) = P((-\infty, x]), \ \ \ x\in\mathbb R, \] pak platí následující věta.
Věta.
Distribuční funkce \(F\) splňuje následující vlastnosti:
Definice. Funkci \(F:\mathbb R\to\mathbb R\) splňující vlastnosti (1) až (3) budeme nazývat distribuční funkcí.
Věta.
Je-li \(F\) distribuční funkcí na reálné ose \(\mathbb R\), potom exisuje na tzv. měřitelném prostoru \((\mathbb R, {\cal B})\) jediná pravděpodobnostní míra \(P:{\cal B}\to\mathbb R\) taková, že
\[
P((a, b])) = F(a) - F(b),
\]
kdykoliv je \(a,b\in\mathbb R,\ -\infty\le a < b<\infty.\)
Důkaz.
Důkaz uvádíme bez důkazu.